לימודי הנדסה רפואית
הנדסה רפואית משלבת יסודות הנדסיים ומדעיים במטרה למצוא פתרונות טכנולוגיים לצרכים רפואיים: אבחון וטיפול במחלות, שיקום ושיפור איכות חיים של מטופלים; מערכות לאבחון וטיפול מרחוק; עיבוד מידע רפואי; פיתוח שתלים; שיטות ריפוי חדשניות; מחקר רפואי מתקדם ועוד.
לימודי תואר ראשון בהנדסה רפואית באפקה מקנים למהנדסים לעתיד ידע אקדמי וכישורים לפיתוח קריירה בתחום.
בוגרי אפקה מסיימים עם הבנה מקיפה, הכוללת באופן ייחודי גם התייחסות להיבטים רגולטוריים, ופרספקטיבה רב-תחומית. בנוסף לכך, במהלך הלימודים מקיימים הסטודנטים קשר עם התעשייה הכולל ביקורים לימודיים במוסדות רפואיים וחברות רלוונטיות.
בלעדי באפקה - סטודנטים הלומדים לתואר ראשון בהנדסה רפואית נהנים מיתרון ייחודי: בכל אחת מן ההתמחויות יכולים הסטודנטים להשתתף בקורסי בחירה במסגרת החטיבה הקלינית. השלמת הקורסים מעניקה לבוגרי התואר תעודה קלינית, תחום חדשני וייחודי העונה על צרכי התעשייה משלב היזמות ועד הכנסת המוצר לשוק.
קרא עודייחודיות תואר ראשון בהנדסה רפואית
היתרונות העיקריים בתואר ראשון בהנדסה רפואית במכללה האקדמית אפקה:
- תעודה קלינית נוספת וייחודית לאפקה בסיום התואר. בזכות קורסים הנלמדים בשתי ההתמחויות אשר עוסקים בעולמות ההנדסה הקלינית ומקנים כלים לניהול מערכות טכנו־רפואיות, לתכנון ובקרה של ניסויים קליניים, ידע בניהול לוגיסטי של פיתוח מוצר חדש ועוד, מקבלים הסטודנטים עם סיום התואר תעודה נוספת.
- סגל מרצים שהם מומחים בעלי שם מהתעשייה והאקדמיה;
- למידה בקבוצות קטנות וקבלת ליווי אישי של חברי הסגל;
- צבירת ניסיון מעשי נרחב – קורסים יישומיים במעבדות, סיורים ושיתופי פעולה עם מכונים, מרכזים רפואיים ותעשיית ההנדסה הרפואית ובפעילויות העשרה נוספות;
- בחירה בין שתי התמחויות הנוגעות בהיבטים הפרקטיים של התחום: הנדסת מערכות מידע רפואיות ומכניקה של מערכות פיזיולוגיות;
- פרויקט גמר המעניק התנסות אמיתית במחקר, בתכנון ובפיתוח מערכת, בבניית אב-טיפוס, בבניית מודלים הנדרשים ממהנדסים רפואיים בתעשייה ועוד;
- קשר אישי עם בוגרות ובוגרים ועם אנשי ונשות תעשייה מהתחום. בזכות שילוב זה, לימודי התואר הראשון בהנדסה רפואית מקנים למהנדסים ולמהנדסות יכולת להשתלב בקלות בתעשייה ולהתקדם בה במהירות
- "סקילבוס" – תוכנית לימודים המשלבת הקניית כישורים חיוניים לשוק העבודה, כגון עבודה בצוות רב-תחומי, למידה עצמית ויכולת תקשורת אפקטיבית;
מסלולי התמחות לתואר ראשון בהנדסה רפואית
מידע נוסף ללימודי .B.Sc בהנדסה רפואית
תקצירי קורסים בתואר ראשון בהנדסה רפואית
קורז זה נלמד ברוב התארים במכללה להנדסה. המספרים הממשיים. פונקציות. סדרות. גבול של סדרה. גבולות ורציפות. משפט ערכי הביניים ומשפט Weierstrass . הנגזרת וחשבון נגזרות. משפט Fermat, משפט Rolle, משפט Lagrange, כלל l'Hopital. שימושים: עליה וירידה, קודות קיצון, קמירות, קעירות ונקודת פיתול. נוסחת Taylor עם שארית Lagrange. חקירת פונקציות. אינטגרל לא מסוים ואינטגרל מסוים ׁׁ(אינטגרל Riemann). המשפט היסודי של החשבון האינטגרלי ונוסחת Newton-Leibniz. שיטות אינטגרציה. אינטגרל לא אמיתי, קריטריוני השוואה.
בוגרי ובוגרות הקורס יהיו מסוגלים/ות להמיר בעיה חישובית לתוכנית מחשב בשפת פייתון, על ידי שימוש בעקרונות התכנות הבסיסיים – שימוש במשפטי תנאי ולולאות, שימוש במבנים סטנדרטים, עבודה עם פונקציות ופונקציות עזר, תרשים זרימה אלגוריתמי לצורך פתרון בעיות חישוביות. יבינו מהי סיבוכיות חישובית וילמדו לפתור בעיות בצורה יעילה חישובית.
הקורס בנוי מ-3 חלקים: כימיה כללית, כימיה אורגנית וביוכימיה: כימיה: אטום, יסוד ואיזוטופים. הטבלה המחזורית. יון, קטיון ואניון. תרכובת ומולקולה. תערובות הומוגניות והטרוגניות. תכונות פיזיקליות וכימיות. השיטה המטרית. המרת יחידות. טמפרטורה וסקלת Kelvin. מול-mole. מסה מולרית. נוסחה כימית – אמפירית ומולקולרית. משוואה כימית. עקרון שימור המסה ואיזון משוואה כימית. תמיסה, חומרים מסיסים וריכוז. חוקי הגזים: חוק בויל, חוק שארל, עקרון אבוגדרו, משוואת הגזים האידיאליים. נפח מולרי. הסטויכיומטריה של גזים בתגובה כימית. צפיפות של גז. איפוזיה. התורה הקינטית של הגזים. מבנה האטום. ספטרוסקופית אור. הדואליות של האור. האפקט הפוטואלקטרי, רמות אנרגיה ומשוואת רידברג. היערכות אלקטרונית של אטומים מרובי אלקטרונים. היערכות אלקטרונית של אניונים וקטיונים. רדיוס אטומי, רדיוס יוני, אנרגיית יינון וזיקה אלקטרונית. היתכנות קשר כימי. קשר יוני, קשר קוולנטי, קשר מתכתי. סדר הקשר. חומצות ובסיסים. חישוב pH. כימיה אורגנית: פחמימנים. תגובות התמרה ואלימינציה. נומנקלטורה. קבוצות פונקציונליות. איזומרים. פולימרים, אלסטומרים וחומרים מרוכבים. ביוכימיה: חלבונים, סוכרים, ליפידים וחומצות גרעין - מבנה, סוגים ופעילויות ביולוגיות, תהליכי יצירה ופירוק. אנזימים - מבנה, פעילות והקשר ביניהם, שמות אנזימים, מעכבי אנזימים, אנזימים אלוסטריים.
וקטורים, מושגי יסוד בקינמטיקה: מהירות ותאוצה, פירוק התאוצה לרכיב נורמלי ומשיקי, תנועה מעגלית, תנועה יחסית, חוקי ניוטון, כוחות בסיסיים, כוחות תלויי זמן, עבודה, אנרגיה קינטית ופוטנציאלית, משפט שימור האנרגיה, משפט מרכז המסה וחוק שימור התנע, תורת הכבידה, תנע זוויתי, תנועה הרמונית, מבוא לתנועת גוף קשיח.
מושגים בסיסיים בהסתברות: מרחב מדגם ומשפטים בסיסיים, חישובים קומבינטוריים, הסתברויות מותנות ואי תלות,משתנים מקריים בדידים ורציפים, תוחלת ושונות של משתנה מקרי, משתנים בעלי התפלגויות מיוחדות, משתנים רב ממדיים ומשפט הגבול המרכזי. מושגים בסיסיים בסטטיסטיקה: בעיות עמידה ובדיקת השערות במודלים הסתברותיים בדידים ורציפים.
הכרת עקרונות שרטוט ההנדסי של גופים מכנים, היטלים, איזומטריה, מישורי עזר, מבט נוסף. הצגת פרקי מכונות לפי תקנים שונים. חיתוך גופים הנדסיים . סימנים מוסכמים בשרטוט, רישום מידות, דרישות דיוק. שימוש בחלקים סטנדרטיים. בניית חלקים מורכבים. הרכבות, מידות בהרכבות, אופן הצגת הרכבה. הכרת סביבת העבודה של תוכנת SOLIDWORKS בניית מודלים תלת ממדיים כמוצקים SOLIDPART הרכבות: קריאת שרטוטי הרכבה, הרכבות BOTTOM –TOP , TOP - BOTTOM הפקת גיליון שרטוט סטנדרטי, EXPLODED VIEW , רשימת חלקים, תיקיית הרכבה.
לימודי הנדסה רפואית כוללים לימודי אלגברה ליניארית. בקורס נלמד על מערכות משוואות ליניאריות – שיטות פתרון ומשמעות. חשבון מטריצות, ישומי חשבון מטריצות לפתרונות של מערכות משוואות. מרחבים וקטוריים והעתקות ליניאריות, ישומי חשבון מטריצות לתיאור העתקות ליניאריות, לכסון מטריצות. מכפלה פנימית, תכונות וישומים של מכפלה פנימית.
רפואה לא פולשנית. אבחון, ניטור וטיפול רפואי. אולטראסאונד: הדמיה, מדידת זרימה וטיפול, שימושים בקרדיולוגיה וגינקולוגיה, גלי הלם.
רנטגן וCT: שימושים בצנטורים, אבחון שברים וגידולים, ממוגרפיה.MRI: אבחון וטיפול בגידולים.
fMRI: מעקב אחר פעילות מוחית. רפואה גרעינית: שימושים בקרדיולוגיה ואונקולוגיה (BRACHYTHERAPHY) . מצלמה בגלולה – שידורים מתוך מערכת העיכול.
ניטור לא פולשני באמצעות מכשירים המבוססים על עקרונות פיסיקליים שונים. הכרת התחומים וחשיבותם של עיבוד תמונות ועיבוד אותות ביולוגיים. הכרת תחום הנדסת רקמות.
מערכות מידע רפואיות, רפואה מרחוק: עיבוד, מיחשוב, איחסון. טכנולוגיות מתקדמות בקרדיולוגיה (סטנטים, לייזרים, לב מלאכותי, וכו').
מכשירים נישאים המבוססים על עיבוד אותות ביומטריים (עין ביונית, אוזן ביונית, קוצב+דפיברילטור,ועוד).
עבור כל שיטה ילמדו העקרונות הפיסיקליים, המיכשור ושימושים ברפואה.
יינתן מבוא פיזיולוגי להבנת המערכות הרפואיות, כנדרש.
"חם מהתנור" – טכנולוגיות רפואיות חדשניות, הנמצאות בשלבי פיתוח וכניסה לשימוש קליני.
הסבר כל שיטה ילווה בהדגמות והמחשות מהקליניקה, המחקר והתעשיות הישראליות.
לימודי הנדסה בתל אביב, כוללים בין היתר קורסים במתמטיקה. טורים. טורי חזקות. פונקציות של מס' משתנים. גבולות ורציפות. נגזרת חלקית ומכוונת. קירובים ליניאריים. גרדיאנט. כלל השרשרת. נגזרות חלקיות מסדר שני, קירוב ריבועי ופולינום Taylor של פונקציות של מס' משתנים. נקודות קיצון מקומיים/מוחלטים. כופלי Lagrange. אינטגרלים מרובים. משפט Fubini. החלפת משתנים ויעקוביאן (Jacobi). אינטגרלים קווים ומשטחיים. אי-תלות אינטגרל קווי במסילה ומשפט Green. משפט Gauss-Ostrogradski ומשפט Stokes.
התא הוא יחידה מורכבת ודינמית המהווה את הבסיס לחיים של יצורים חד ורב-תאים. נושאי הקורס כוללים: מולקולות אורגניות (מבט כללי בלבד), מבנה קרומים ביולוגיים ואברוני התא, שלד התא, צמתים בין תאיים והחומר החוץ תאי ( ECM). תהליכים שילמדו כוללים: הומיאוסטאזיס, סינתזה ופירוק חומרים בתא , הובלה דרך ממברנות והובלה בין מדורי התא, נשימה תאית, רצפטורים ותקשורת בין תאים. תאי מערכת החיסון ישמשו כמודל לתקשורת ושיתוף פעולה בין תאי. נושאים נוספים שינתן להם דגש הם גנטיקה מולקולארית, מחזור התא, מיטוזה, מיוזה והפריה, תאי גזע והתמיינות, הזדקנות ומוות תאים, התא הסרטני.
מיון משוואות דיפרנציאליות. משוואות דיפרנציאליות מסדר ראשון. משוואות דיפרנציאליות לינאריות מסדר n: משוואה הומוגנית ואי-הומוגנית, Wronskian משוואות הומוגניות עם מקדמים קבועים. הפרדה לבעיה הומוגנית ואי-הומוגנית, שיטת המקדמים הלא ידועים ושיטת וריאצית פרמטרים. בעיות שפה – תורת Sturm Liouville : הגדרת אופרטור צמוד לעצמו, מציאת ערכים עצמיים ופנקציות עצמיות של האופרטור והוכחת תכונותיהן. מערכת של משוואות דיפרנציאליות לינאריות מסדר 1: פתרון המערכת ההומוגנית באמצעות ערכים עצמיים ווקטורים עצמיים של המטריצה. ה- Wronskian של המערכת. המערכת האי-הומוגנית.
פונקציות מרוכבות כולל חישוב אינטגרלים קוויים, שימוש שיטות "מרוכבות" לחישוב אינטגרלים ממשיים. שימושים בהתמרות אינטגרליות – של Fourier, Laplace.
כוח חשמלי. מטען חשמלי. חוק קולון. חוק שימור מטען. עקרון הסופרפוזיציה. השדה החשמלי. קווי השדה. צפיפות מטען קווית, משטחית ונפחית. חישוב השדה בעזרת אינטגרציה. שטף וחוק גאוס. העבודה בשדה חשמלי. פוטנציאל חשמלי ומתח. חישוב הפוטנציאל כאינטגרל של השדה החשמלי. השדה החשמלי כגרדיאנט של הפוטנציאל. משטחים שווי פוטנציאל. אנרגיה פוטנציאלית חשמלית. מוליכים, מבודדים ותכונותיהם. קבל. קיבול. אנרגיה של השדה החשמלי. חומרים דיאלקטריים בקבלים. חיבורי קבלים. זרם חשמלי. צפיפות הזרם. התנגדות ומוליכות. תופעת העל-מוליכות. חוק אום. כא"מ. חיבורי נגדים. הספק חשמלי. מעגל RC. מגנטיות. כוח מגנטי על מטען. השדה המגנטי. כוח לורנץ. כוח מגנטי על תיל נושא זרם. חוק ביו-סבר. חישוב שדה מגנטי. תכונות מגנטיות של חומרים. חוק אמפר. חוק גאוס לשדה מגנטי. השראה. כא"מ מושרה. חוק פרדיי. חוק לנץ. השראה עצמית. זרם העתקה. משוואות מקסוול בצורתן האינטגרלית.
נושאי הקורס העיקריים כוללים מבוא לאנליזה וקטורית, שיווי משקל של חלקיקים במישור ובמרחב, מערכת של כוחות ומומנטים, מערכות שקולות, שיווי משקל של גוף קשיח המישור ובמרחב, מערכת של גופים, מרכז כובד של שטחים, כוחות מפולגים, מומנטי אנרציה של השטח, צירים ראשיים ומומנטי שטח ראשיים, כוחות פנימיים ודיאגרמת כוחות ומומנטים.
מעגלים ואלמנטים מקובצים: תיאור הרכיבים הפסיביים, קשרים פיסיקליים בין משתני מתח, זרם ומטען. מאפייני אותות ומקורות מתח וזרם. חוקי שימור: חוקי קירכהוף. טופולגיות חיבור ומעגלים שקולים במעגלים בזרם ישר וזרם חילופין. הספקים. מעבר כוכב-משולש, גשר ויטסטון ונגד משתנה. העברת הספק מרבי. תיקון מקדם הספק. שיטות לניתוח מעגל חשמלי מרובה מקורות בלתי תלויים: זרמי חוגים, מתחי צמתים, שיטת ההרכבה, שקול נורטון ותבנין. תגובת תדר, מעגלי תהודה טוריים ומקביליים. אלמנטים מצומדים, שנאים ומנועים.
משוואות מיתר מאולץ. שיטת D'Alembert למיתר אינסופי, החזרת גלים בקצה קשור ובקצה חופשי. מוצגות היטב. מיון משוואות לינאריות שני. צורות קנוניות. משוואות לפלס. פתרון משוואת מיתר סופי ומאולץ ע"י הפרדת משתנים. הוכחת יחידות הפתרון למשוואת הגלים בשיטת האנרגיה. עקרון המקסימום. מוצגות היטב של בעיית Dirichlet . הפרדת משתנים למשוואת לפלס בתחום מלבני ובעיגול. משוואת החום. עקרון המקסימום למשוואת החום ופתרון בעזרת הפרדת משתנים. פתרון המשוואה הלא הומוגנית. פתרון משוואות חלקיות ע"י התמרות אינטגרליות. תנודות חופשיות בממברנה עגולה ומשוואת בסל.
הקורס מתמקד בתורת הקוונטים ובהקשר זה גם בתורת היחסות הפרטית. הנושאים העקריים: משבר הפיסיקה הקלסית, מהירות האור, ניסוי מייכלסון-מורלי, עקרונות של תורת היחסות הפרטית, טרנספורמצית לורנץ, התכווצות האורך, התארכות הזמן. בו זמניות, חיבור מהירויות. תנע ואנרגיה יחסותיים, מסת מנוחה ואנרגית מנוחה, התנגשויות והתפרקויות. גלים אלקטרומגנטיים, קרינת גוף שחור, האפקט הפוטואלקטרי, פוטונים, פיזור קומפטון, גלי דה ברויי - דואליות גל-חלקיק, ספקטרום אטומי, מודל בוהר, רמות אנרגיה, ניסוי פרנק-הרץ, עקרון אי-הוודאות, משוואת שרדינגר, פונקציית גל והמשמעות ההסתברותית שלה, משוואת שרדינגר הסטציונרית, חלקיק בבור פוטנציאל, קוונטיזציה של האנרגיה, מדרגת פוטנציאל, מחסום פוטנציאל, תופעות קוונטיות, מינהור, בור פוטנציאל תלת ממדי, אורביטלים אטומיים ומולקולריים, אופרטורים, פונקציות עצמיות וערכי תוחלת.
מבנה ופעילות מערכת העיכול, בקרת מטבוליזים של סוכרים, שומנים וחלבונים, בקרת איזון אנרגטי כללי, הבלוטות ההורמונליות העיקריות, פעילותן וויסות פעילותן, מבנה הכליות ופעילותן, ופיסיולוגיה של מערכת החיסון (אימונולוגיה). דגש מיוחד יינתן לפעילות ולאינטגרציה בין חלקי הגוף השונים ברמות ארגון שונות ולמנגנוני הבקרה ההומיאוסטטים.
בקורס נשתמש בפיתון לעבוד נתונים, ביצוע פעולות על מערכים, עיבוד אות ותמונה. בהמשך, נכיר את מטלב ונלמד לבצע פעולות דומות בשפה זו- פעולות אריתמטיות בסיסיות, שימוש במטריצות, פונקציות , גרפיקה עיבוד אות ותמונה כמפורט בטבלה לפי שבועות.
מבוא, הגדרת מאמץ, הגדרת מעוות, חוק הוק, עומס צירי, מאמצי מתיחה, לחיצה, גזירה ומעיכה. פיתול, כפיפה, כוחות גזירה בקורות, פיתוח משוואת מאמצי הגזירה בחתך הקורה, מיקום מאמץ הגזירה המקסימאלי ועוצמתו, מאמצים משולבים.
טורי פוריה: פיתוח לטור פוריה בקטע סופי, מקדמי פוריה. הצורה המרוכבת של טורי פוריה. התכנסות הטור, פונקצית Dirichlet , התכנסות בנקודת קפיצה. תופעת Gibbs . הזהות של פרסוול. התמרת פוריה, הגדרה, תכונות וטבלת הטרנספורם. שימושי התמרת פוריה בעיבוד אותות ובפתרון משוואות דיפרנציאליות. התמרת Laplace ושימושיה בפתרון משוואות דיפרנציאליות. פתרון המשוואה באמצעות התמרת לפלס במקרים בהם פונקצית האילוץ היא פונקצית מדרגה ופונקצית דלתא.
כל לימודי תואר ראשון בכמללת אפקה כוללים ביקורים במעבדות המקצועיות שלנו. סדרי עבודה וכללי בטיחות. מדידות ומכשירי מדידה. תורת השגיאות. מערכת מולטילב. עיבוד נתוני ניסויים. ביצוע ניסויים בשלוש גישות שונות, (א) ניסויים במתכונת מודרכת. (ב) ניסויים במתכונת חצי עצמאית. (ג) ניסויים במתכונת עצמאית - ביצוע ניסויים מתוך מאגר רחב של ניסויים במגוון נושאים שונים.
הולכה חשמלית ומערכת העצבים המרכזית וההיקפית. פעילות השריריים, צימוד עצב-שריר. מערכת הלב וכלי-דם: ההולכה החשמלית בלב, הפעילות המכנית של הלב, המערכת כלי הדם הכליליים, בקרת וויסות פעילות הלב, מחזור הדם: קטרים, לחצים וספיקות בכלי הדם העורקיים והורידיים, ויסות זרימת הדם, זרימה במיקרוצירקולציה הפריפרית. מערכת הנשימה: אוורור ופרפוזיה, ויסות הנשימה, צימוד פעולת לב-ריאה. מערכת הרבייה הנקבית והזכרית: מהזקיק ועד הלידה, השבחת זרע, הפריית מבחנה, שימור תאי גזע עובריים. העין: מבנה ותפקוד, האוזן: מבנה ותפקוד. ויסות חום הגוף. עבור כל מערכת ילמדו המבנה והתפקוד מנקודת מבטו של המהנדס, תוך הדגשת הפעילות המכנית והאותות הפיזיולוגיים הנוצרים בגוף (לדוגמא: אותות מכאניים, חשמליים, אופטיים , אקוסטיים ומגנטיים).
הגדרות, מערכת תרמודינמית ונפח בקרה, תכונותיו של חומר ומצבי צבירה שונים, ממדים ויחידות, שיווי משקל, חוק האפס של התרמודינמיקה, תהליכים תרמודינמיים, משוואת המצב, גזים אידיאליים, עבודה וחום. החוק הראשון של התרמודינמיקה למערכת ולנפח בקרה. מושגי האנרגיה הפנימית, האנטלפיה וחום סגולי, החוק השני של התרמודינמיקה, מושג האנטרופיה, תהליך הפיך, מחזור קרנו, החוק השני למערכת ולנפח בקרה, מחזורים תרמודינמיים בסיסיים.
מושג הגל, משוואת הגלים במיתר, פתרונות כלליים, עקרון הסופרפוזיציה,גלים נעים כלליים, גלים נעים הרמוניים, גלים עומדים, אופני התנודה במיתר סופי,הצגת גל כלוא במיתר על ידי טורי פורייה, מקדמי מעבר והחזרה , גלי קול בגז,עוצמה בגל, מיתרי הקול, האוזן, גלי קול ברקמות ביולוגיות, אפקט דופלר, התאבכות. משוואות מקסוול בהצגה דיפרנציאלית, גלים אלקטרומגנטיים, גלים מישוריים,צפיפות אנרגיה, וקטור פוינטינג, לחץ קרינה, קיטוב
סדרי עבודה במעבדת חשמל. כללי בטיחות. מכשירי מדידה בתחום חשמל ומגנטיות. מדידות. חיישני זרם ומתח של מערכת מולטילוג. ביצוע ניסויים בשלוש גישות שונות, (א) ניסויים במתכונת מודרכת. (ב) ניסויים במתכונת חצי עצמאית. (ג) ניסויים במתכונת עצמאית - ביצוע ניסויים מתוך מאגר רחב של ניסויים במגוון נושאים שונים.
מוליכים למחצה, דיודות, דוגמאות מעשיות לשימוש בדיודות, דיודות זנר ומייצבים, ספקים לינאריים. טרנזיסטורים: בי פולרי ותוצא שדה - ניתוח DC ו - AC, מקורות זרם, מעגלי הגברה, מגברי שרת.
מושגי יסוד, הידרוסטאטיקה וקינמטיקה. פיתוח ושימוש במשוואת השימור לנפח בקרה ובמשוואות הדיפרנציאליות השולטות בשדה הזרימה. פיתוח כלים לחישובי הפסדים וגרר בזרימות תמידיות.
מושגי יסוד במכשור רפואי: רקע היסטורי,טרמינולוגיה, מבנה כללי של מערכות מדידה וטיפול ביו-רפואיות, אפיון של מערכות מדידה רפואיות, סיווג של מכשור ביו-רפואי. ניתוח מתמטי ומעגלים אלקטרוניים השקולים למערכות מדידה ביו-מכניות, ביו-זרימה וחום. מדידת של פוטנציאלים ביולוגיים, אלקטרודות ומעגלים אלקטרוניים. מדידת טמפרטורה בעזרת תרמיסטור, צמד תרמי וקרינה באינפרא אדום. מדידת משתנים מכניים כמו העתקה, מהירות, תאוצה, כוח, לחץ וזרימה בעזרת מתמרים התנגדותיים, קיבוליים, השראותיים, פייזוחשמליים ופייזוהתנגדותיים. עקרונות של מערכות תמיכה בחיים בחוג סגור מבוססות חיישנים. בטיחות חשמל ובעיות רגולטוריות במערכות מדידה רפואיות.
בקורס יוצגו עקרונות ה-DSP ומימושם. בין הנושאים שילמדו: ייצוג אותות בזמן בדיד, תורת הדגימה, התמרת פורייה בזמן בדיד ו –FFT, מסננים דיגיטליים, מסנני IIR ו-FIR.
אינטרפולציה: שיטות לגרנז' וניוטון, אינטרפולציה הרמיטית, ספליין. גזירה נומרית. אינטגרציה נומרית: שיטת הטרפז, סימפסון ונקודת האמצע. שיטות האינטגרציה לפי גאוס. קירוב ריבועים מינימליים. קירוב לפתרון משוואה דיפרנציאלית: שיטות טיילור,הון ורונגה קוטה, שיטות סתומות. קירוב לפתרון משוואה לא ליניארית ,שיטת החצייה, שיטת ניוטון-רפסון , מיתר ושיטות איטרטיביות של נקודת השבת. קירוב לפתרון מערכת משוואות ליניארית: שיטת הדירוג של גאוס, מוצגות של מטריצה, שיטות איטרטיביות ופירוק LU.
שום הנלמד בקורסים התיאורטיים באמצעות סדרת ניסויים הממחישים תופעות פיזיולוגיות באמצעות מכשירי מדידה שונים. במסגרת הקורס תשולב מעבדה הכוללת ניסויים המבוססים על ניתוח ואפיון מתמרים בסיסיים כגון, ניטור מדידות ספיקת אוויר, רווית חמצן וטמפרטורת גוף, ניטור פוטנציאלים חשמליים מהלב ECG, המוח EEG ושריר שלדEMG . הסמינר כולל ניתוח האותות הנמדדים לרבות השוואה בין מצבים פיזיולוגים שונים (כגון, מנוחה ומאמץ), יחסי-גומלין של מדדים שונים, אנליזת תדרים של האותות הנמדדים, תכנון ניסוי וכתיבת דו"ח מדעי מפורט: תקציר - תיאור המחקר, רקע, שיטות המחקר, תוצאות, דיון וסיכום. הצגת התוצאות ישולבו כמטלת הצגת המחקר בפוסטר מדעי בקורס "מכניקה פיזיולוגית של מערכת השלד והשרירים". שפת הוראה של הקורס : אנגלית
תואר בהנדסה רפואית במכללת אפקה כולל מגוון קורסים מקצועיים, ביניהם קורס עיבוד וזיהוי תמונה. מערכת הראייה האנושית, מאפייני תמונה ספרתית והבסיס לעיבוד תמונה (בינארי, רמות אפור), ניתוח פורייה ועיוותים, דגימה ושיחזור של תמונה, שיפור תמונה בעזרת עיצוב היסטוגרמת רמות האפור, פילטרים שונים לעיבוד ושיפור תמונה, מבוא לתורת האינפורמציה, קידוד ודחיסת מידע בעיבוד תמונות, עקרונות ייצוג ועיבוד של תמונה בצבע, מבוא לעיבוד וידאו, תמונות 3D, יישומים של עיבוד תמונה. מערכת שעות
במהלך הקורס להקניית הידע הבסיסי בנושאי מעבר חום ומסה, יבחנו תהליכי המעבר במערכות ביולוגיות שונות ובשימושים נוספים באבחון ובטיפול בעזרת חוקי שימור ומשוואות מעבר חום ומסה. הנושאים: הקדמה והגדרות, עקרונות מעבר חום- הולכה, הסעה וקרינה, מעבר חום ברקמות ביולוגיות, הולכת חום, חוק פורייה, הסעת חום, מעבר חום בקרינה, מערכות משולבות הולכה והסעה, אנלוגיה חשמלית, בעיות חד-ממדיות במצב עמיד, שימור אנרגיה - משוואת מעבר החום הכללית, תנאי שפה והתחלה. שימור אנרגיה כולל הסעה, משוואת Bioheat transfer ביונקים, מעבר חום במשטחים בולטים, מעבר חום עם Transient condition , מספר Biot . מנגנוני מעבר חומר, הגדרות ריכוזים, קשרי שיווי משקל בין פאזות, ריכוזים בגזים אידיאליים, דיפוזיה, חוק פיק, מעבר חומר בהסעה, אנלוגיות בין מעבר חום ומסה, ממשק נוזל-גז, משוואה שולטת למעבר מסה.
בכל מכללה מקצועית ללימודי הנדסה רפואית צריך להגיש בסיום התואר פרויקט גמר. סדנת פרויקט הגמר תלווה את הסטודנטים בשלבים השונים של פרויקט הגמר: במהלך סמסטר ב' תסייע הסדנה בהגדרה מפורטת של מהות הפרויקט, האתגר ההנדסי, המטרות, היעדים והמדדים, חלופות לביצוע הפרויקט, תכן ראשוני, בניית תוכנית עבודה והגדרת תוצרי הפרויקט. במהלך הסדנה ילמדו הנהלים, הכוללים את אופן העבודה העצמאית ועבודה מול מנחה הפרויקט, אבני הדרך, המטלות והציונים. במהלך הסדנא תינתן הכשרה בנושאים שונים לרבות יכולות פרזנטציה אפקטיבית של נושאים הנדסיים והיבטים שונים של תוצרי פרויקט הגמר.
הנושאים העיקריים המועברים בקורס כוללים סקירה היסטורית על התפתחות הביומכניקה, מבנה ותפקידי מערכת השלד, סוגי העצמות ותכונותיהם הביומכניות, אלסטיות לינארית, סוגי מפרקים, תכונות ותפקידי שרירי השלד, ויסקואלסטיות לינארית, תיאור המפרקים העיקריים בגוף האדם, שיווי משקל סטטי במפרקים, קינמטיקה של גוף האדם, דינמיקה של גוף האדם, אנליזה של הליכה.
מבוא, אינטראקציה בין קרינה (אלקטרו-מגנטית, אולטרה-סאונד) ורקמה, קרני X (צילום רנטגן ושיקוף, רדיותרפיה, CT), רפואה גרעינית (צילום דו-מימדי, SPECT, PET, טיפול בקרינת גמא ובקרינת ביתא, radioimmunotherapy ,brachytherapy), MRI (הפיסיקה של MRI, סדרות פולסים ופרוטוקולים, מבנה של סורק, שימושי MRI), אולטרה-סאונד (פיסיקה של US, התמונה, יישומים עיקריים בדימות רפואי, שימושי US לטיפול).
סווג מערכות: מערכות מכניות, חשמליות, תרמיות, נוזליות ומעורבות בעלות אלמנטים מקובצים וקבועים. בניית מעגלים שקולים לרבות דוגמאות מעולם המכשור הרפואי. ניתוח מערכות רציפות במישור הזמן: תגובה לתנאי התחלה, תגובה להלם, קונבולוציה כתגובה לערור שרירותי. ניתוח יסודי של מערכות מסדר ראשון ושני. התמרת לפלס החד צדדית ושימושיה; פונקצית התמסורת, קטבים ואפסים במישור התדר המרוכב. תיאור מערכת במרחב המצב, הצגת משוואות מצב ופתרונן בתחום הזמן ובתחום התדר. תיאור מערכות בעזרת דיאגרמות מלבנים. תגובת תדר לערור סינוסואידלי, דיאגרמות בודה (חזרה). מערכות בדידות: קבלת משוואות הפרש ופתרונן בתחום הזמן, תגובה לתנאי התחלה ומשפט הקונבולוציה הבדידה. מערכות משוב, יציבות של מערכות משוב: קריטריוני נייקויסט ובודה, אנליזה באמצעות מקום גיאומטרי של שורשים, דיאגרמת ניקולס. אפיון מערכות משוב בתחום הזמן ובתחום התדר, שגיאת מצב מתמיד ושגיאה חולפת. קריטריונים: מקדמי שגיאה, רגישות, שיכוך הפרעות, רוחב סרט. מערכות בקרה פיזיולוגיות, בקרת מערכות הנדסיות הנמצאות באינטראקציה עם מערכות פיסיולוגיות.
ייצוג מידע - מספרים, פעולות אריתמטיות, קודים. אלגברה בוליאנית. מעגלים לוגיים קומבינטוריים. מימוש מעגלים לוגיים קומבינטוריים: מעגלים אריתמטיים (מסכם מלא, מסכם בינרי מקבילי, מסכם עשרוני, כופל), מבנה יחידה אריתמטית לוגית (ALU), משווה, מרבב, מקודד. רכיבים מיתכנתים: זכרון קריאה בלבד (ROM),PLA,PAL. מעגלי עקיבה אסינכרוניים. מעגלי עקיבה סינכרוניים. מימוש מעגלי עקיבה ב-MSI ו-LSI: רגיסטר מקבילי, רגיסטר הזזה, מונה אסינכרוני וסינכרוני, יחידת זכרון קריאה/כתיבה (RAM). מבנה יחידת עיבוד מרכזית (CPU). מכשור רפואי משובץ מיקרו-מחשבים. מעגלים ואותות (סיגנלים) לוגיים – הגדרות: סיגנלים לוגיים, רמות לוגיות, משפחות לוגיות, מהפך בסיסי, פרמטרים של מעגל לוגי אופייני: אופיין תמסורת, חסינות לרעש, פיזור הספק סטטי ודינמי. התנהגות בזמן :זמני תגובה של שער, זמן עליה, זמן ירידה, מכפלת השהייה-הספק. דלגלגים – SR-FF, D-FF, JK-FF, Master-Slave, מעגלים מרובי פאזות, רגיסטרי הזזה ומונים, סינכרון בין שעונים ו- Metastate. לוגיקה דינמית – רגיסטרי הזזה אנלוגיים: CCD, Bucket Brigade, רגיסטרי הזזה, שערים, מפענחים דינמיים, PLAs. תאי זכרון – תאי SRAM, DRAM, ROM, PROM, EPROM, E²PROM . מגברי חישה. מעגלים ספרתיים ביפולריים – אפיון פונקציית תמסורת של שערים של משפחות סטנדרטיות: ECL, LSTTL, TTL. Fan-In ו- Fan-Out. מעגלי קטימה וריתוק. שימוש בנ"ל במכשור רפואי ספרתי.
החלק הראשון של הקורס יעסוק בשפת C, ייצוגים בינאריים ומניפולציה שלהם, היכרות בסיסית אך רחבה של סביבת פיתוח התוכנה Labwindows CVI וכתיבת תוכנות מחשב בעלות יכולות מתקדמות עם ממשק משתמש גרפי. החלק השני כולל הכרת הארדואינו, תקשורת עם הארדואינו. החלק השלישי יכלול כתיבה וקריאה של אותו דיגיטליים ואנלוגיים, יישום של שיטות בקרה שונות הן בחוג פתוח והן בחוג סגור (on/off, PID). הקורס כולל לכל אורכו תרגול רציף של הסטודנטים בכתיבה מעשית ויישום מלא ובחינה של הנלמד בקורס.
קורס זה מציג עקרונות בסיסיים בשימוש בסימולציות נומריות להנדסה. הקורס כולל הכרה של השיטות הבסיסיות המקובלות (והפרשים סופיים ואלמנטים סופיים), ופיתוח מיומנויות במידול מייצג של בעיה הנדסית, עיבוד התוצאות ודיווח. הקורס כולל שימוש בתוכנות מסחריות (כגון ANSYS) ומציג שיקולים בבניית מודל חישובי מבחינת הנחות, הערכת שגיאה, רישות, התכנסות ואופטימיזציה של משאבי מחשב. בנוסף תוצגנה שיטות לפתרון בעיות מצומדות (לדוגמה: מבנה –זרימה), מודלים ביורפואיים.
חלקו הראשון של הקורס עוסק בפתולוגיה כללית, דהינו בתהליכים החולניים הבסיסיים של הגוף החי כמו נמק, דלקת או יצירת גידול. תחילה ילמדו מושגים בסיסים בפתולוגיה ושיטות מעבדה בסיסיות ולאחר מכן נעסוק בגורמיםובמנגנונים המובילים להיווצרותן והתפתחותן של תהליכים חולניים, בשינויים הפתולוגים המופיעים ברקמות ובסימנים הקליניים. בקורס גם יסקרו קבוצות הפתוגנים השונות עם דגש על דרכי הדבקה, גורמי אלימות והפתוגנזה. חלקו השני של הקורס (פתולוגיה מערכתית) יעסוק במספר מצומצם של מחלות ספציפיות (כמו סכרת מסוג 1 ואוטם שריר הלב). המנגנונים הפתולוגים שנלמדו בחלקו הראשון של הקורס יקושרו למערכות ולאיברים הרלוונטיים עם דגש על השינויים הספציפיים לאיבר והשפעתם על הגוף כולו.
מורפולוגיה מתמטית, סגמנטציה, אנליזה של טקסטורה, יישומי זיהוי תבניות לעיבוד תמונה, Fuzzy Logic, רשתות נוירונים, רגיסטרציה של תמונות, אנליזה של תנועה, תמונות 3D רפואיות.
בחלקו הראשון של הקורס תינתן הדרכה אודות מהות העבודה הסמינריונית, כללי כתיבה אקדמית ומתודיקה של העברת מצגות. בהמשך יבחרו נושאי העבודות ותינתן הדרכה פרטנית. חלקו השני של הקורס מבוסס על עבודה עצמאית של הסטודנטים: גיבוש העבודה הסמינריונית, לרבות סקר ספרות, ניתוח ביקורתי של המאמרים , הסקת מסקנות וכתיבת העבודה. זאת תוך הדרכה וליווי פרטניים, בהתאם לנדרש. הצגת העבודות לרבות דיונים בכתה המבוססים על עבודות אלו. חלקו השלישי של הקורס כולל עריכת העבודה במתכונת של מאמר סקירה מדעי, וכתיבה בהתאם להנחיות כתב העת המתאים לנושא הסמינריון. זאת תוך הדרכה וליווי פרטניים.
מערכות הזרימה הביולוגית; ריאולוגיה של הדם; זרימה פועמת בצינורות קשיחים וגמישים; התפצלויות, חיבורים והיצרויות; מאמצי גזירה על דופן כלי הדם; התנגדות ואימפדנס במערכת כלי הדם, התפשטות גלי הלחץ והחזרים; זרימה בקפילרות; זרימות בלב, מודלים ואנלוגיות חשמליות, זרימות פתולוגיות; זרימות במערכת הנשימה; זרימות במערכת הלימפתית והכלייתית. סקר ספרות לטכנולוגיות חדשניות, העמקה והצגה במסגרת דיבייט.
פרויקטי גמר נבחרים
-

מערכת לניתוח אותות PPG לצורך זיהוי הפרעות קצב לב ומעקב אחר מצב הבריאות | מאת: ספיר נדיר ומאיה ששו
מערכת קומפקטית ולבישה למדידת אותות PPG לזמן ארוך ולשימוש עצמי, לצורך זיהוי הפרעות בקצב הלב ואבחון מצב בריאות כללי של המשתמש.
מערכת קומפקטית ולבישה למדידת אותות PPG לזמן ארוך ולשימוש עצמי, לצורך זיהוי הפרעות בקצב הלב ואבחון מצב בריאות כללי של המשתמש.
-

זיהוי פתלוגיות בכלי דם באמצעות סימולטור זרימה לאולטרסאונד | מאת: יובל אשכנזי נרזנוי
פרויקט מחקרי שמטרתו לזהות פתלוגיות בכלי דם על ידי שיטות מתחום הלמידה חישובית.
פרויקט מחקרי שמטרתו לזהות פתלוגיות בכלי דם על ידי שיטות מתחום הלמידה חישובית.
-

Pillow-Care | מאת: צח סידי ורוני משולם
פיתוח אב-טיפוס של מערכת כריות אשר מתממשקת למחשב ומספקת משוב למשתמש על תנוחות הישיבה שלו.
פיתוח אב-טיפוס של מערכת כריות אשר מתממשקת למחשב ומספקת משוב למשתמש על…
-

אפיון הידרוג'ל היברידי הנוצר בתהליך הרכבה עצמית ומורכב מפפטיד המשולב עם ג'לטין לאחר הדפסה תלת מימדית | מאת: עומר עמרים
ייצור ואפיון הידרוג'ל היברידי חדש המורכב מג'לטין ו- FmocFF, אשר ניתן להדפיס אותו במדפסת תלת-ממד ובכך להשתמש בו בהמשך כדיו-ביולוגי
ייצור ואפיון הידרוג'ל היברידי חדש המורכב מג'לטין ו- FmocFF, אשר ניתן ל…
-

זיהוי רטינופתיה סוכרתית באמצעות סמארטפון | מאת: ירדן גלבוע
בדיקה שמגלה רטינופתיה סוכרתית (מחלת רשתית) אצל חולי סכרת, שהיא הגורם מספר אחד לעיוורון בעולם.
בדיקה שמגלה רטינופתיה סוכרתית (מחלת רשתית) אצל חולי סכרת, שהיא הגורם מ…
-
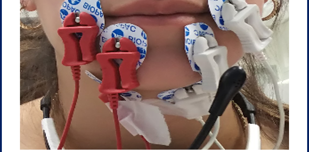
זיהוי דיבור בעזרת מדידות חשמליות משרירי הפנים | מאת: שרית מלייב
פיתוח שיטה לזיהוי דיבור שקט מתוך מדידות חשמליות משרירי הפנים. מדידות אלו יוכלו לסייע בפיתוח מכשיר המבצע זיהוי דיבור אוטומטי. המכשיר יעזור לחולים עם פגיעות במיתרי הקול המתקשים לתקשר עם סביבתם או עובדים בסביבה רועשת
פיתוח שיטה לזיהוי דיבור שקט מתוך מדידות חשמליות משרירי הפנים. מדידות א…
ZOOM IN הנדסה רפואית
שאלות ותשובות על תואר ראשון בהנדסה רפואית
הלימודים אורכים בין 4 שנים בהתאם למסלול בו בוחר הסטודנט ללמוד.
לימודי הנדסה רפואית באפקה מתקיימים במסלול יום.
הנדסה רפואית היא תחום המשלב ידע הנדסי עם מדעי הרפואה, במטרה לפתח פתרונות טכנולוגיים בתחום הבריאות. מהנדסות ומהנדסים רפואיים עוסקים בפיתוח פתרונות לאבחון וטיפול רפואי, שתלים, טכנולוגיות טיפוליות, ועוד.
כן! במהלך הלימודים בתואר בהנדסה רפואית, הסטודנטים והסטודנטיות מבצעים פרויקטים מעשיים הכוללים עבודה על פיתוחים טכנולוגיים, בניית אב-טיפוס ומודלים הנדסיים. בנוסף, ישנם קורסים יישומיים במעבדות ופעילויות העשרה הכוללות שיתופי פעולה עם תעשיית ההנדסה הרפואית, מכונים רפואיים ועוד.
שכרו של מהנדס רפואי מתחיל בישראל הוא שכר מתגמל ונחשב לתחרותי ביחס לשוק. שכר זה יכול להשתנות בהתאם למקום העבודה, תחום ההתמחות והמיקום הגיאוגרפי, אך באופן כללי מדובר בשכר גבוה יחסית בתחומי ההנדסה.
לימודי הנדסה רפואית באפקה מציעים יתרונות ייחודיים כמו תעודה קלינית נוספת בסיום התואר, קורסים יישומיים בשיתוף פעולה עם תעשיית ההנדסה הרפואית, פרויקטים מעשיים, סגל מרצים אקדמי בעל ניסיון מהתעשייה, קשרים עם אנשי ונשות מקצוע בתעשייה, ויכולת להתמחות בהנדסת מערכות מידע רפואיות ומכניקה של מערכות פיזיולוגיות.
כן, בוגרי תואר ראשון בהנדסה רפואית יכולים להמשיך לתואר שני בתחומים כמו הנדסה רפואית, הנדסה ביומדית, מדעי המחשב, ניהול מערכות בריאות, ועוד. התואר מספק בסיס מצוין להמשך לימודים אקדמיים בתחום זה או בהרחבה לתחומים קרובים.
הלומדים הנדסה רפואית באפקה יכולים לבחור מבין שני מסלולי התמחות: הנדסת מערכות מידע רפואיות ומכניקה של מערכות פיזיולוגיות.
בשתי ההתמחויות האלה משולבים קורסים מתחום ההנדסה הקלינית המקנים כלים לניהול מערכות טכנו־רפואיות, לתכנון ובקרה של ניסויים קליניים, ידע בניהול לוגיסטי של פיתוח מוצר חדש ועוד.
לימודי ההנדסה הקלינית הם חדשניים, ייחודיים ועונים על צורכי התעשייה הרפואית להובלת מוצר מִשְלב היזמות ועד הכנסתו לשוק, בניהול רגולציה, בתקנים ובמחקרים קליניים. השלמת הקורסים מקנה תעודה נוספת בסיום התואר.
הלימודים באפקה מועברים על ידי סגל מרצים בעלי תואר שלישי (דוקטורט) וניסיון בתעשייה, העוסקים בהוראה ובמחקר ונמנים עם חברי האיגוד הישראלי להנדסה רפואית וביולוגית. הלימודים באפקה מתקיימים בכיתות קטנות מה שמאפשר לכל סטודנט לקבל יחס אישי וליווי צמוד של הסגל.
המונחים "הנדסה רפואית" ו"הנדסה ביו־רפואית" מתייחסים לאותו תחום עיסוק, וההבדלים ביניהם תלויים בעיקר בדגשים של כל מוסד לימודים.
במכללת אפקה, תוכנית הלימודים מתמקדת בהיבטים הפרקטיים של התחום – בדגש על פיתוח מכשור רפואי ומערכות מידע רפואיות. הסטודנטים יכולים לבחור בין שתי התמחויות ייחודיות:
- מכניקה של מערכות פיזיולוגיות – התמחות המכשירה מהנדסים לתכנון, פיתוח וייצור של מכשור רפואי מתקדם לאבחון, טיפול, שיקום ושיפור איכות החיים של מטופלים.
- הנדסת מערכות מידע רפואיות – התמחות המשלבת ידע בהנדסת תוכנה, מערכות מידע והנדסה רפואית, במטרה לענות על הביקוש למהנדסים בתחום זה בתעשייה ובמערכת הבריאות.
בוגרי תואר בהנדסה רפואית יכולים להשתלב בתעשיות רבות, כולל פיתוח מערכות רפואיות, מכשור רפואי, טכנולוגיות אבחון, חברות רפואיות, רפואה מותאמת אישית ועוד. תעשיות אלו כוללות את תחום הטכנולוגיה הרפואית, מכוני מחקר, בתי חולים, חברות יזמיות ופיתוח טכנולוגיות רפואיות חדשניות.
מהנדסים רפואיים מועסקים בתעשיות מגוונות, כולל חברות לפיתוח מכשור רפואי, תעשיית התרופות, חברות טכנולוגיות רפואיות, מכוני מחקר, בתי חולים ומרכזים רפואיים, חברות המפתחות שיטות טיפול חדשניות, יזמים בתחום הבריאות, ועוד.
הצלחה בתחום ההנדסה הרפואית דורשת מיומנויות טכניות בתחום ההנדסה, יכולת פתרון בעיות יצירתית, ידע מעמיק במערכות רפואיות, כישורים בעבודה בצוות רב-תחומי, הבנה רגולטורית, וכן יכולות תקשורת אפקטיביות כדי לשתף פעולה עם רופאים, אנשי מקצוע מהתעשייה והציבור הרחב.
סגל אקדמי
ד"ר שרה נפתלי
מילה מראש בית הספר להנדסה רפואית:

ד"ר שרה נפתלי
מילה מראש בית הספר להנדסה רפואית:
התוכנית לתואר ראשון בהנדסה רפואית כוללת לימודים תאורטיים בתחומי ההנדסה והרפואה, וסיורים במכונים, מרכזים רפואיים ובתעשיית ההנדסה הרפואית. הסטודנטיות והסטודנטים זוכים גם להתנסות מעשית במעבדות המכללה, בהן עמדות מתקדמות המדמות מערכות פיזיולוגיות ומשמשות למדידות של מערכות בגוף. לנוכח המעורבות של אפקה בפעילויות של איגודים מקצועיים ובאקוסיסטם של החברות בתחום, הסטודנטים נחשפים לתעשייה ולשיתופי פעולה שונים ומעשירים, המסייעים להם בהבנת שיטות העבודה הנהוגות בה. סגל התוכנית כולל מרצים בעלי תואר שלישי (דוקטורט) וניסיון בתעשייה, העוסקים בהוראה ובמחקר ונמנים עם חברי האיגוד הישראלי להנדסה רפואית וביולוגית. הם תומכים, מלווים, מייעצים ומכווינים את הסטודנטים לאורך התוכנית.
לכל חברי הסגלצרו קשר
לשכת הנהלה אקדמית
טלפון: 03-7688691/744
פקס: 03-7688692
דוא"ל: AcademicHeadsBox@afeka.ac.il
מחלקת ייעוץ לימודים
ימים א'-ה': 09:00-19:00 | יום ו': 09:00-13:00
חייגו: 1-800-37-37-10 (שלוחה 1)
פקס: 03-7688679
מייל להרשמה: mirsham@afeka.ac.il





























הנדסה רפואית
שתף לינק באמצעות:
https://www.afeka.ac.il/academic-departments/bsc/medical-engineering/WhatsApp
Facebook
Twitter
Email
https://www.afeka.ac.il/academic-departments/bsc/medical-engineering/